All issues

Supplementary information:

Movies of the computer experiments are presented in the form of GIF animations (Visualizations 1-16). GIF animations are started and restarted automatically. To be able to stop a movie on a specific iteration, you need to download the movie and open it in a video player, for example, in Media Player Classic. Each movie demonstrates iterations of a cellular automaton with the number of individuals on the lattice at each iteration.

Visualization 1. Model 1 with Moore neighborhood.

Visualization 2. Model 1 with hexagonal neighborhood.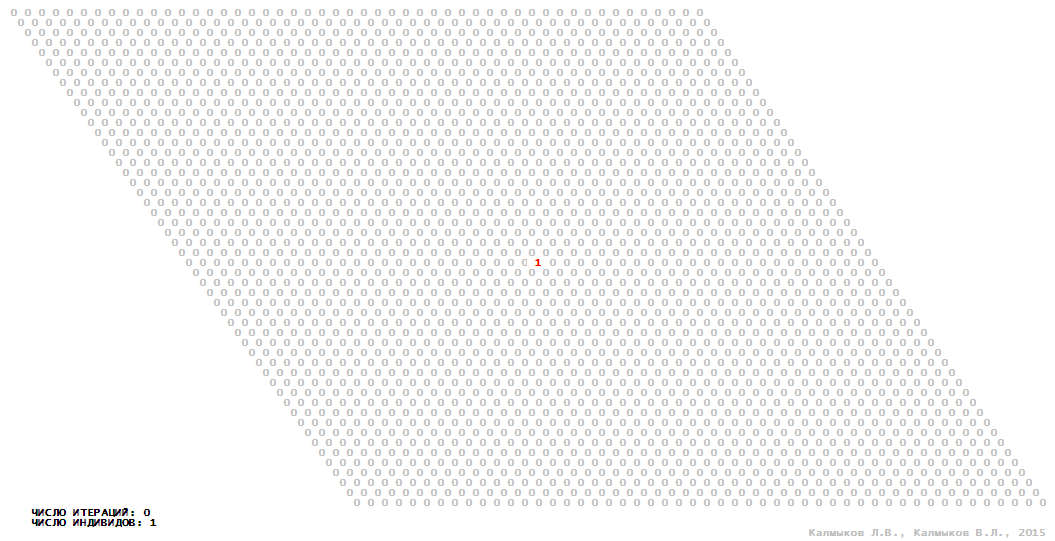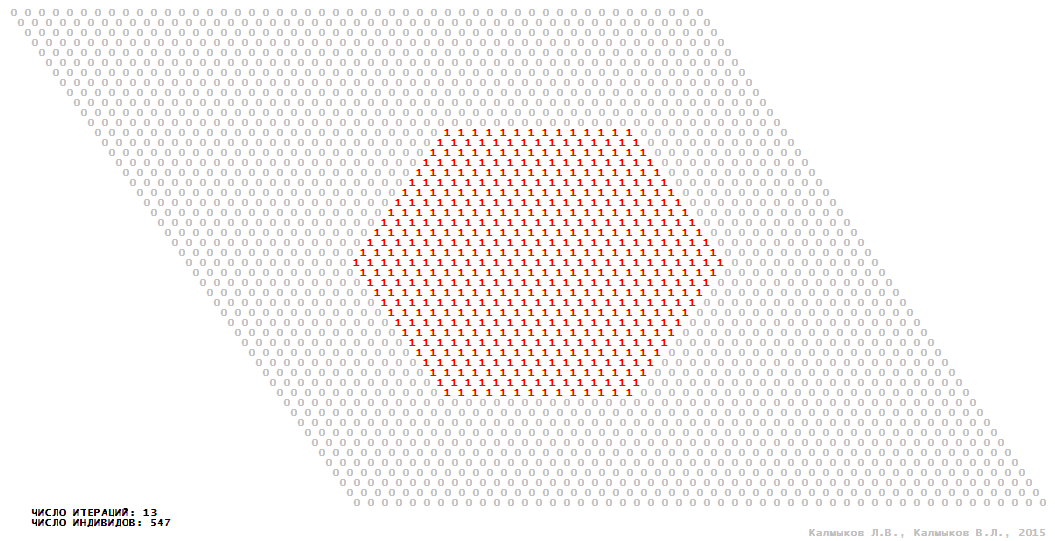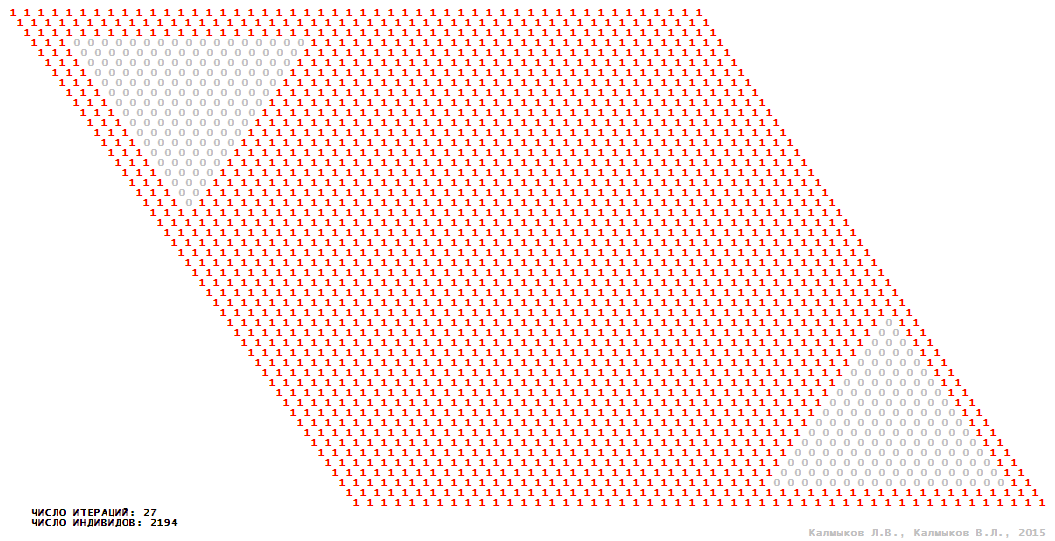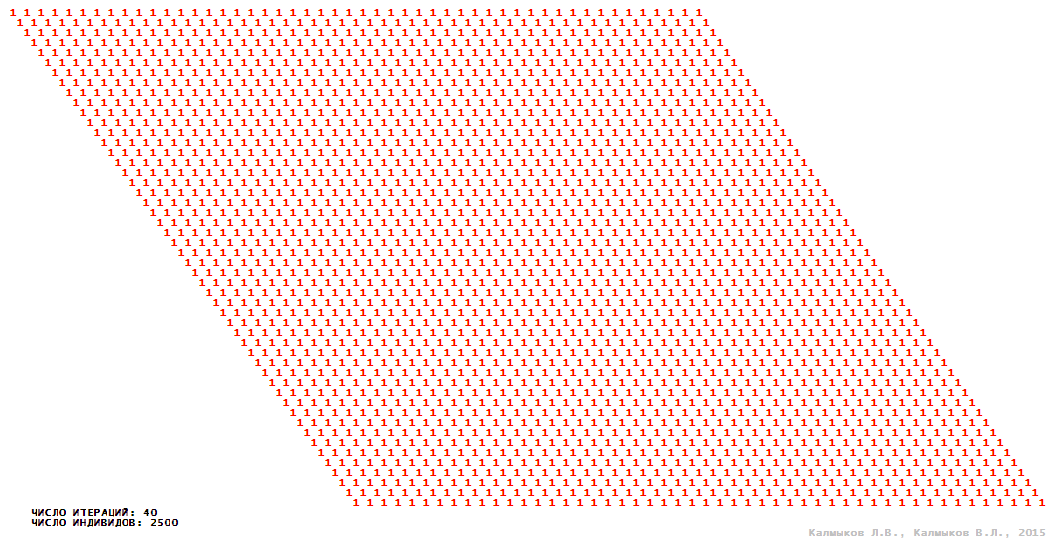

Visualization 3. Model 1 with von Neumann neighborhood.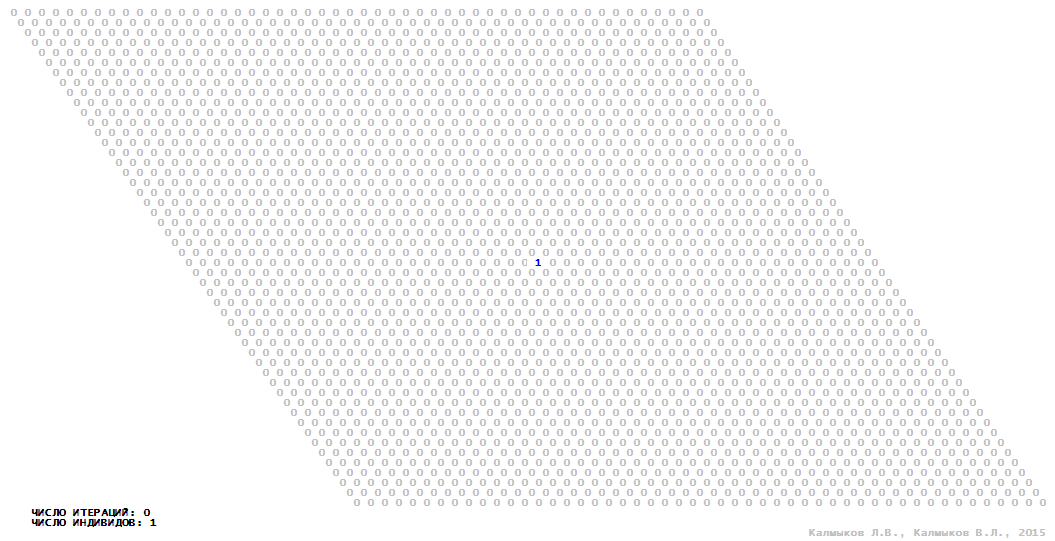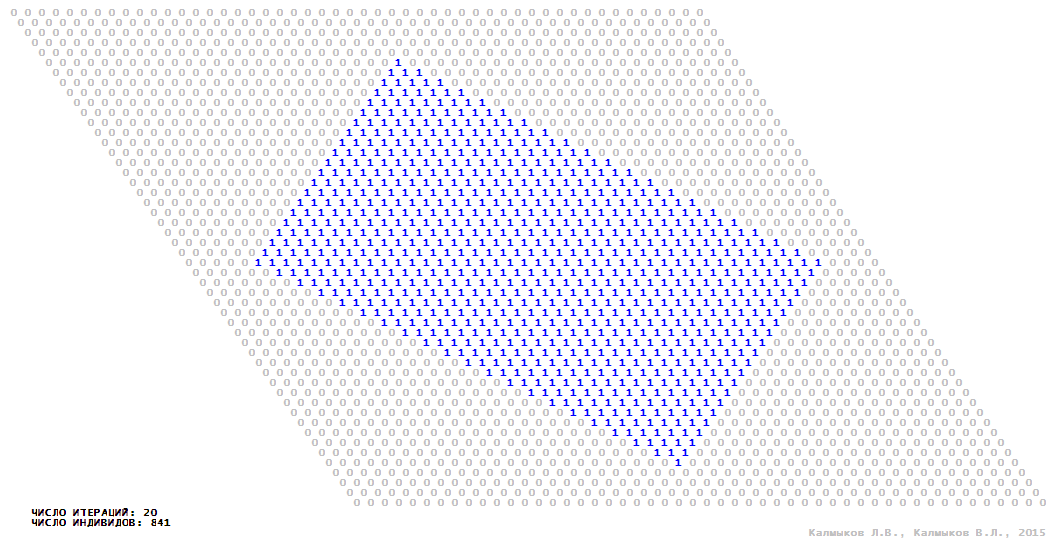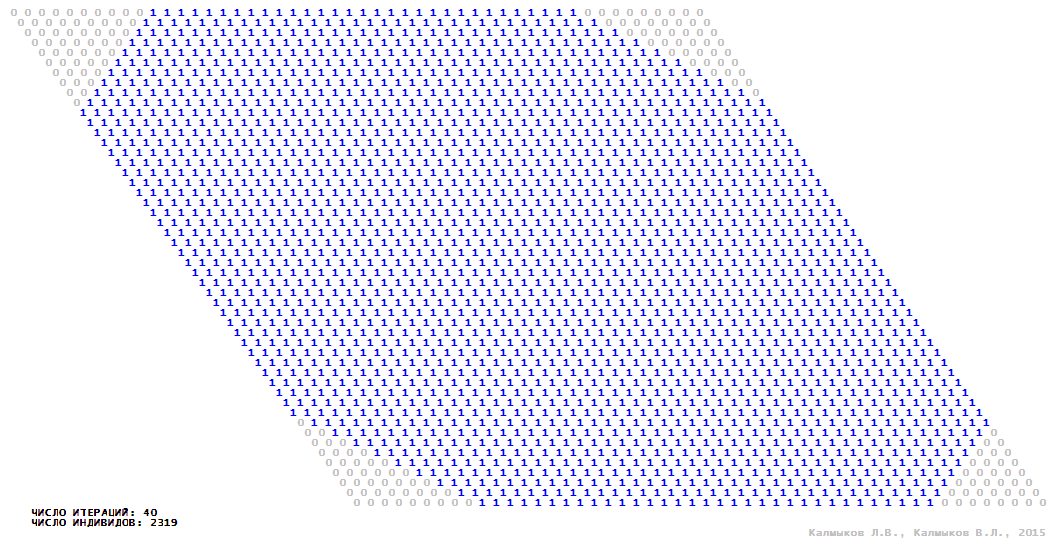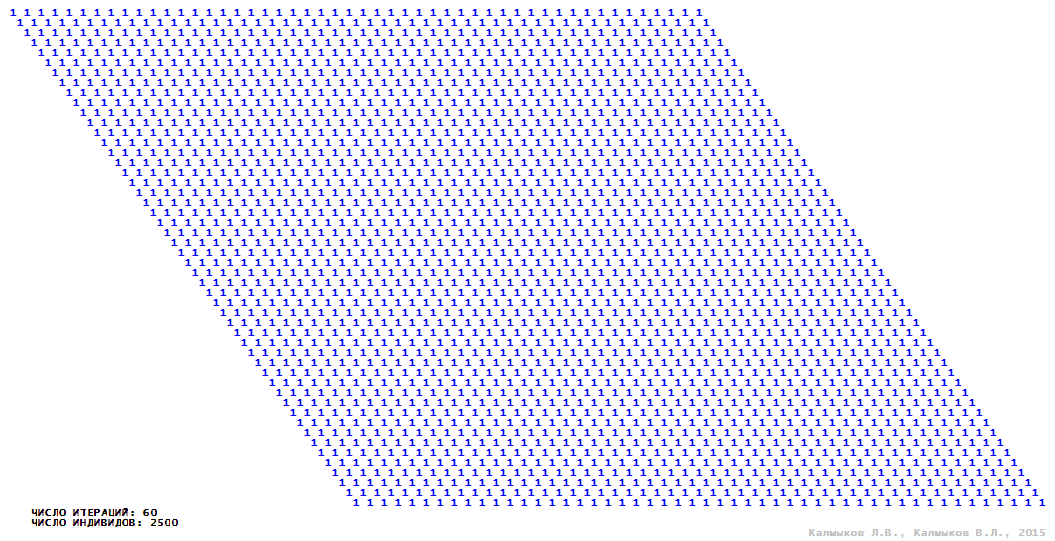

Visualization 4. Model 1 with tripod neighborhood.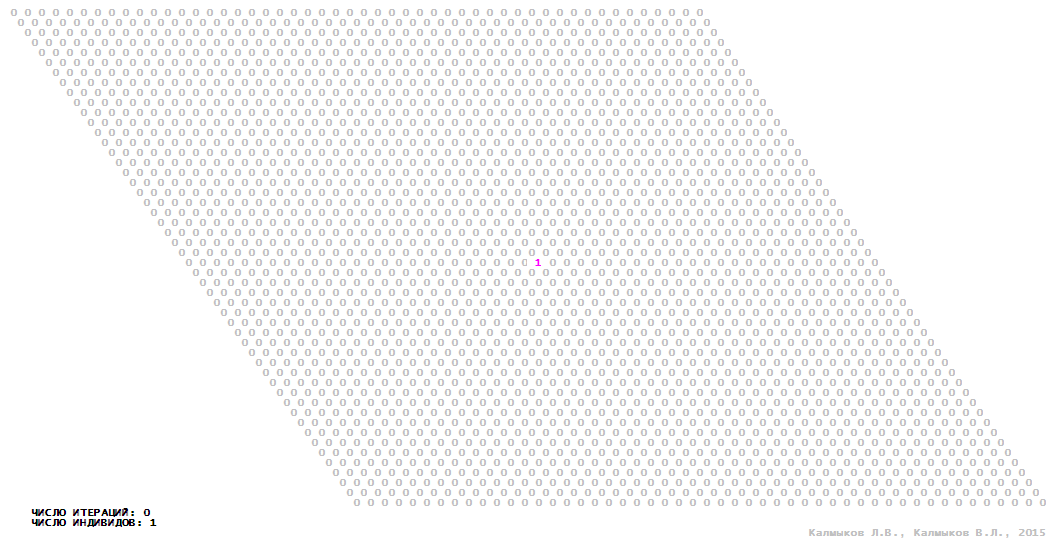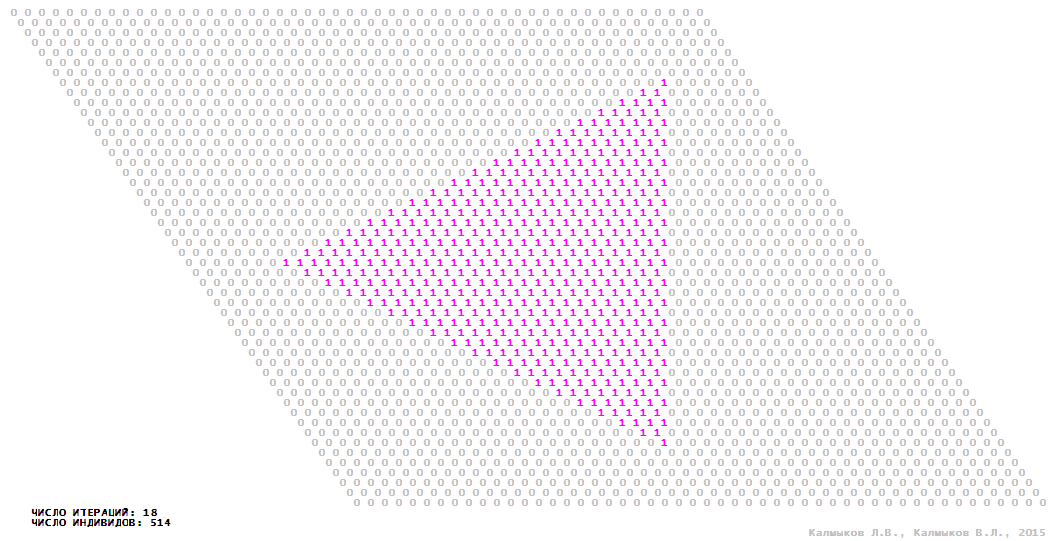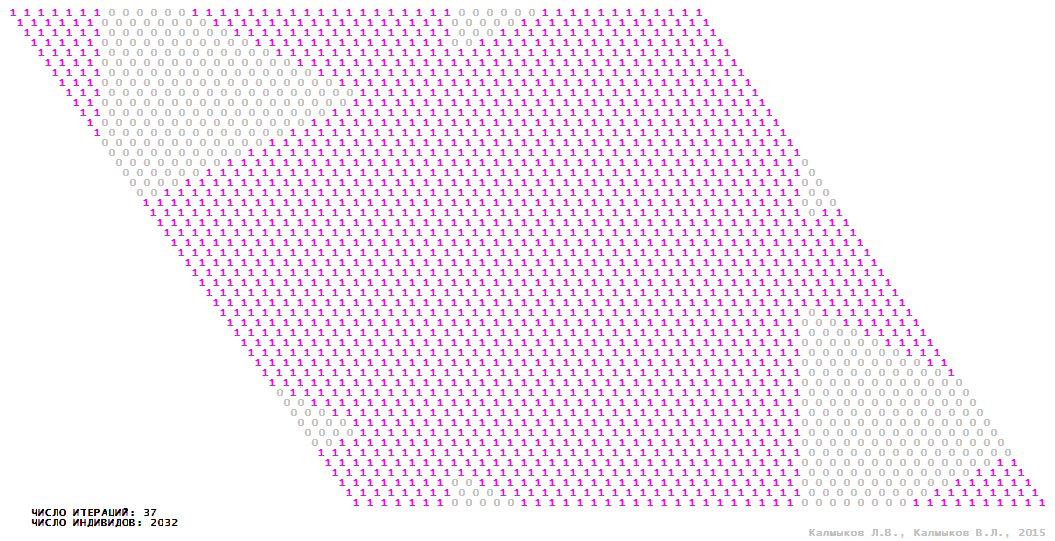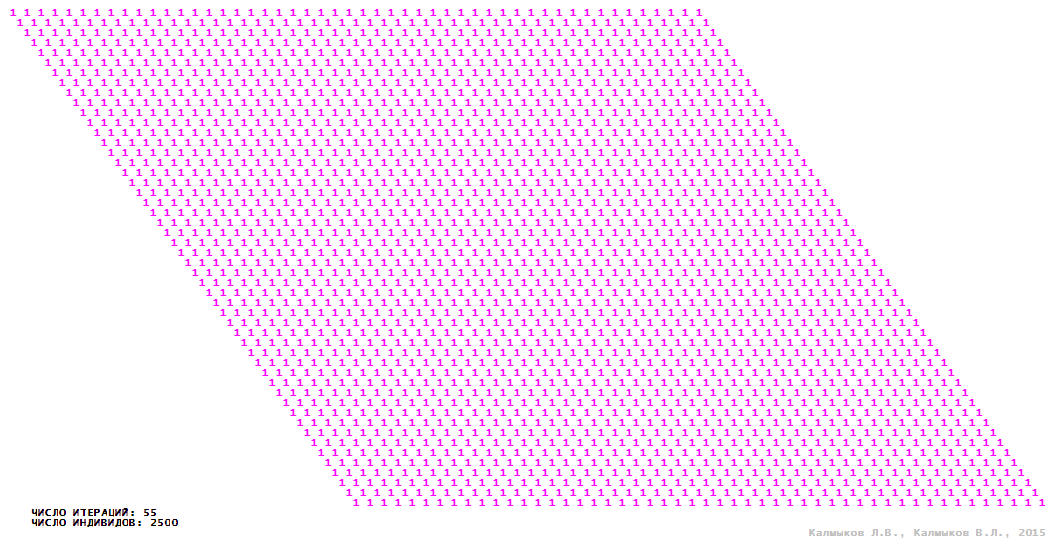

Model 1 (Visualizations 1–4) is a logical deterministic cellular automaton with two states. A set of possible states of each lattice site is {0, 1}. Cellular automaton lattice consists of 50x50 sites and it is closed by periodic conditions on the torus. Resource regeneration of a microhabitat and recycling of a dead individual occur simultaneously with life activity of a new individual which has occupied this microhabitat. The following symbols are used to indicate the states of cellular automaton cell: {0} – a microhabitat is free; {1} – a microhabitat is occupied by an individual. Using various neighborhoods we investigate the impact of the number of offsprings and of their positioning in space on population dynamics. Population growth curves have S-shaped form and are shown in Figure 10a. In all four cases a successful colonization of free habitat occurred and species continued to exist indefinitely long.

Visualization 5. Model 2 with Moore neighborhood.

Visualization 6. Model 2 with hexagonal neighborhood.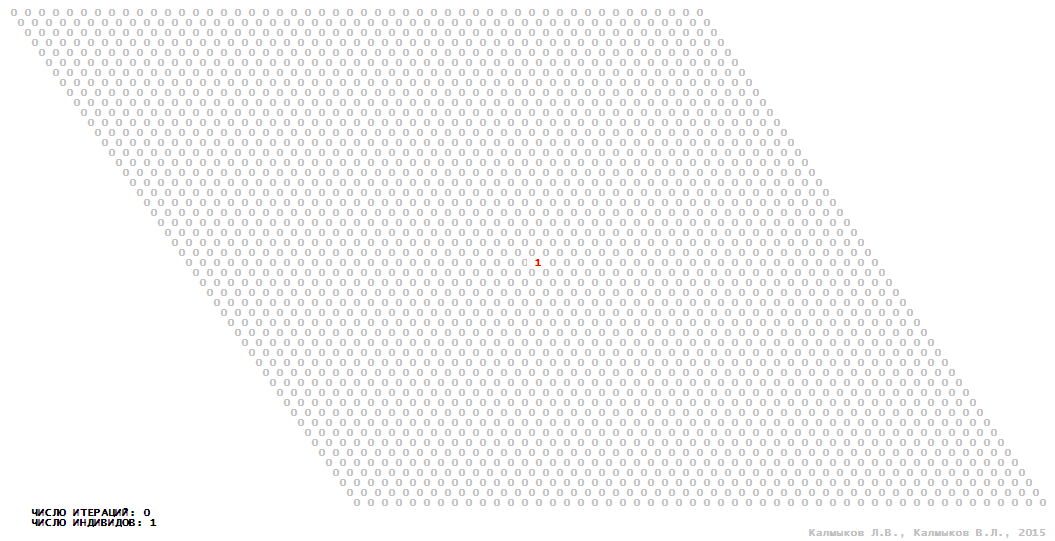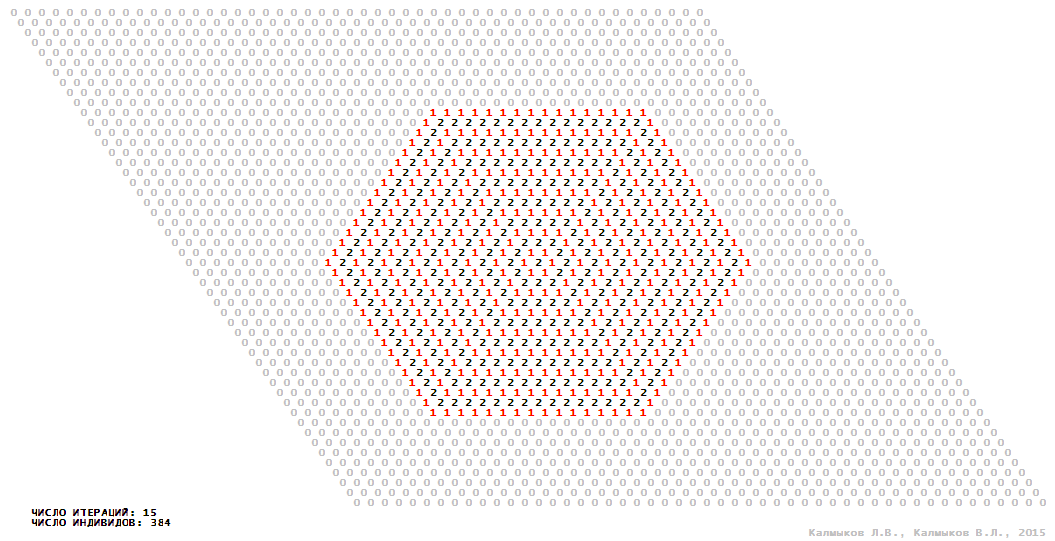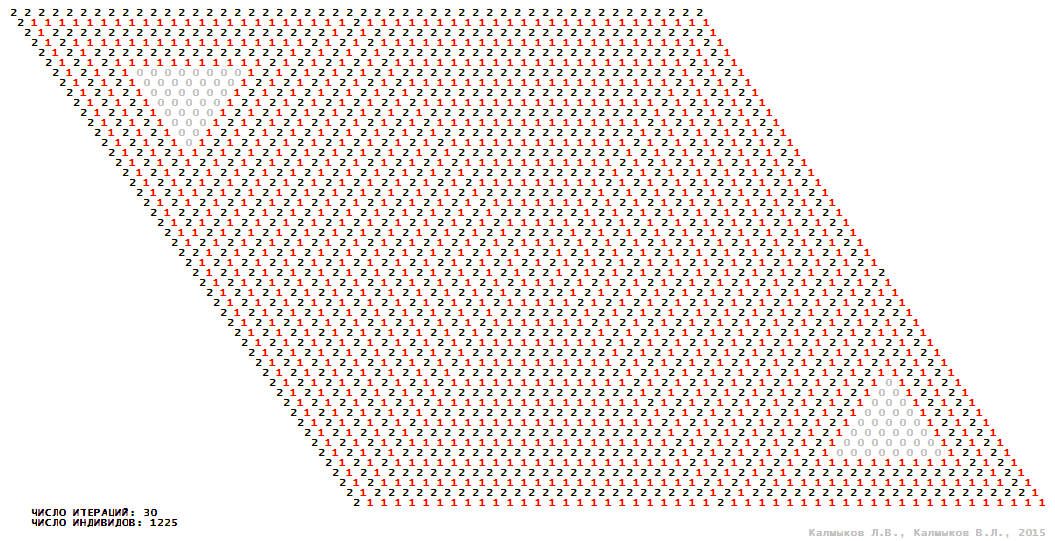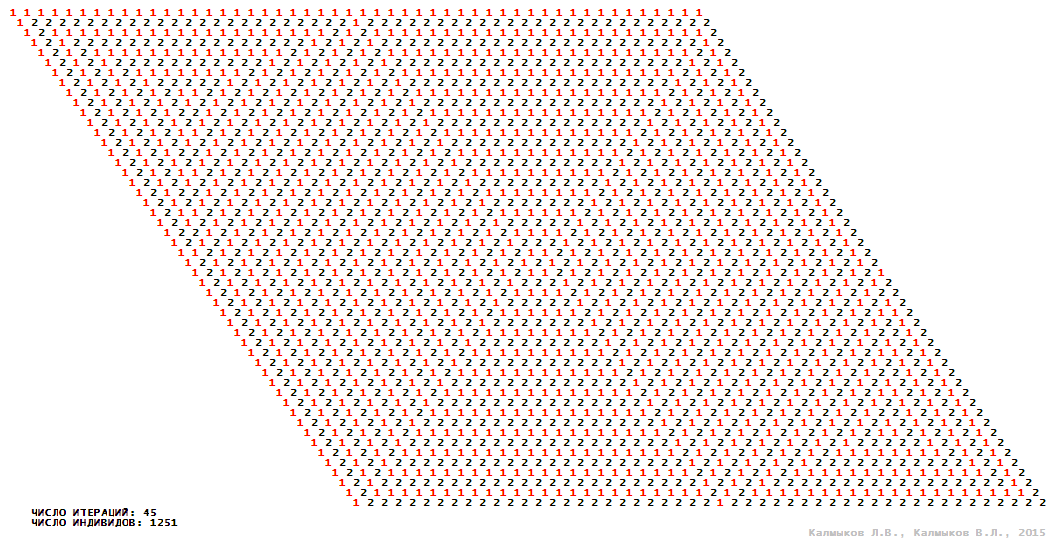

Visualization 7. Model 2 with von Neumann neighborhood.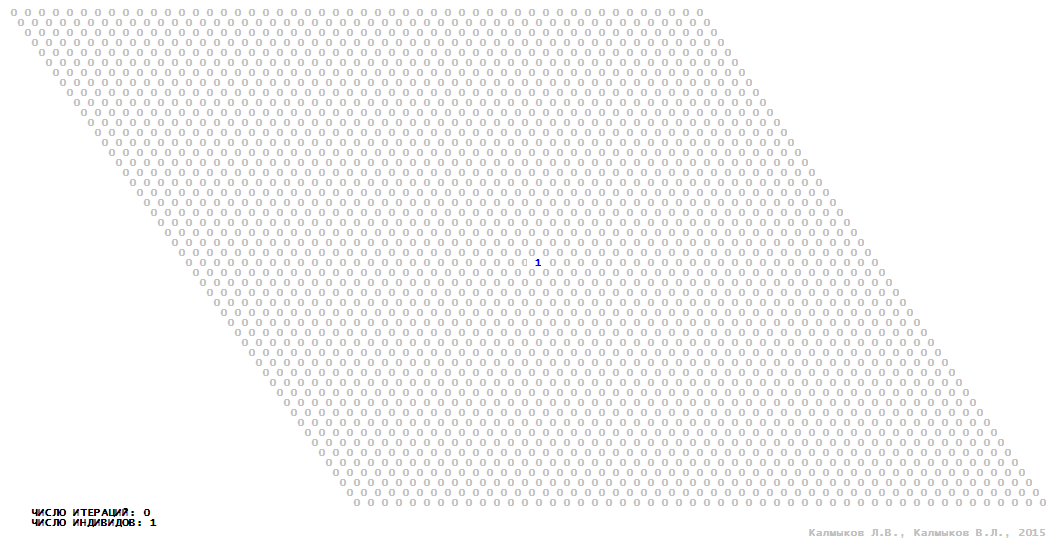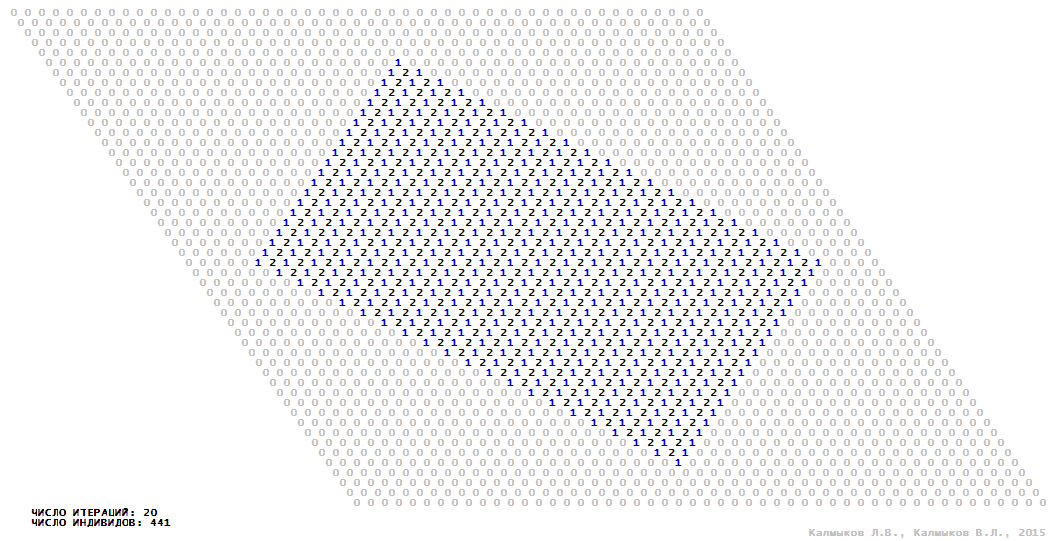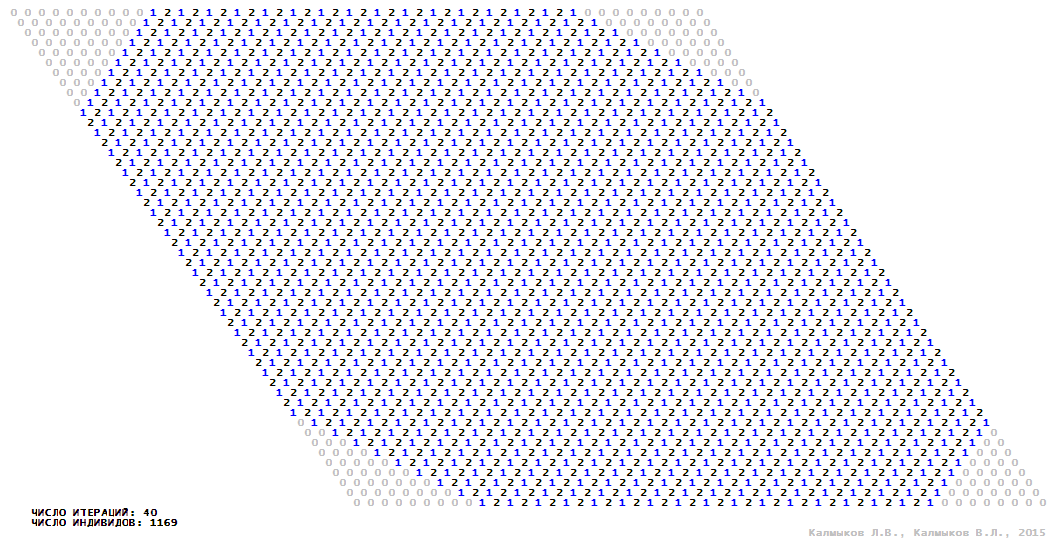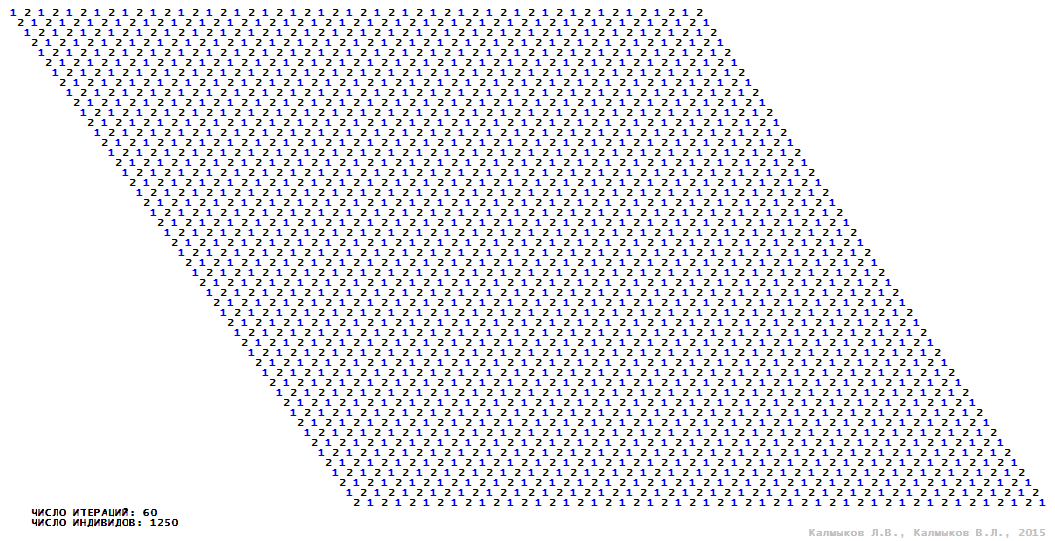

Visualization 8. Model 2 with tripod neighborhood.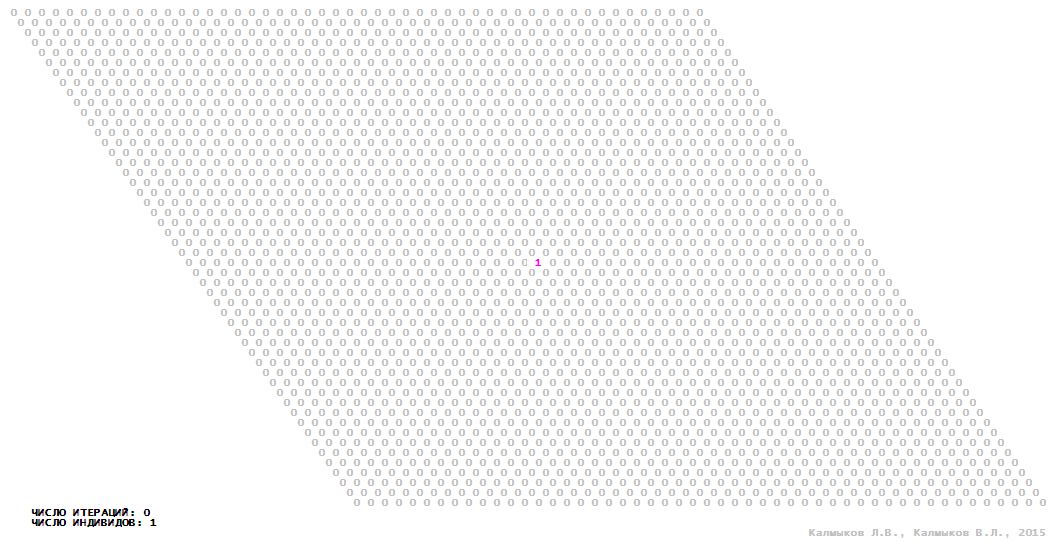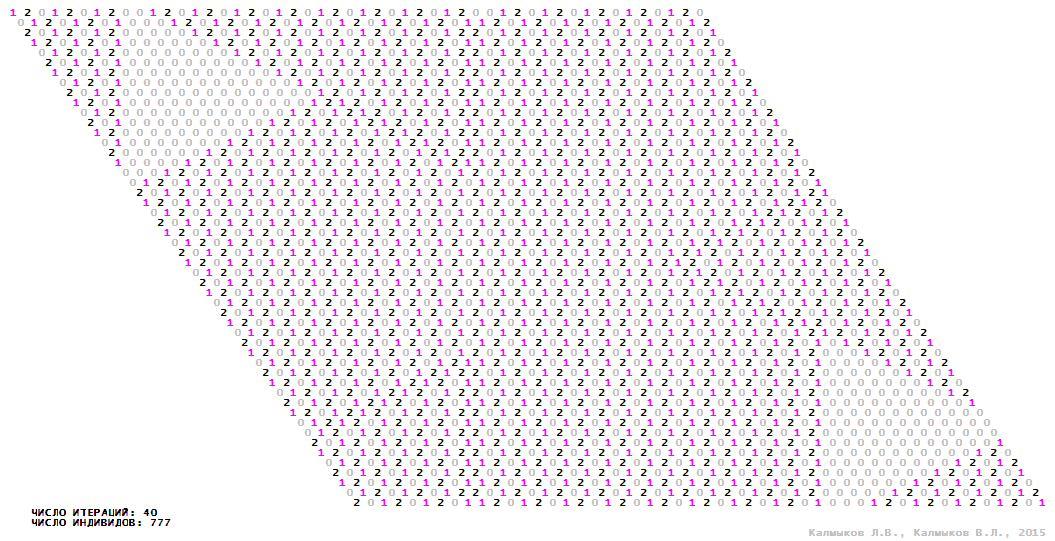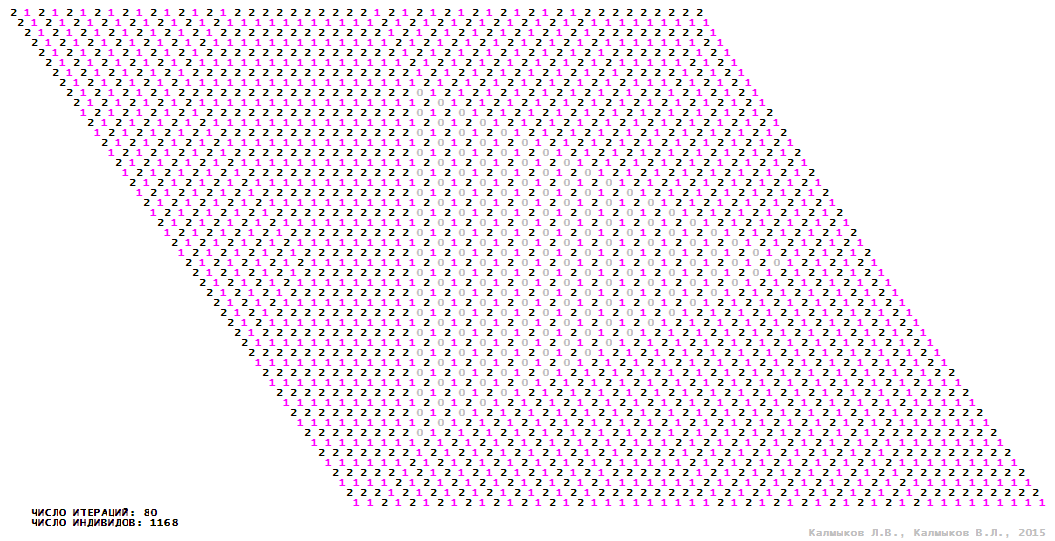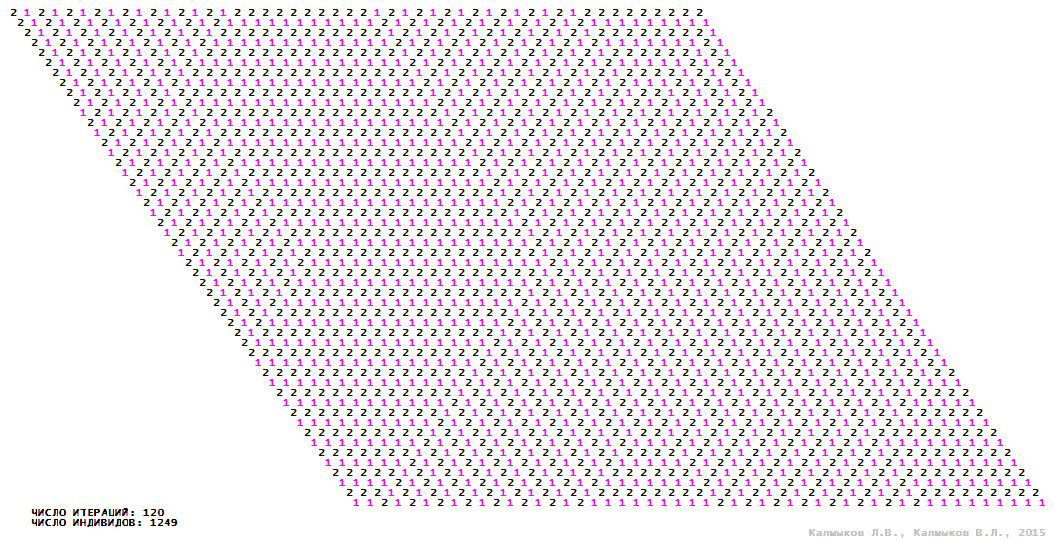

Model 2 (Visualizations 5–8) is a logical deterministic cellular automaton withthree states. A set of possible states of each lattice site is {0, 1, 2}. Cellular automaton lattice consists of 50x50 sites and it is closed by periodic conditions on the torus. Resource regeneration of a microhabitat includingrecycling of a dead individual takesone iteration. The following symbols are used to indicate the states of cellular automaton cell: {0} – a microhabitat is free; {1} – a microhabitat is occupied by an individual; {2} – a microhabitat is in the regeneration state which takes one iteration. Using various neighborhoods we investigate the impact of the number of offsprings and their positioning in space on population dynamics. Population growth curves have S-shaped formwhenMoore, hexagonal and von Neumann neighborhoods are used (Fig. 10б). Population growth curve has double S-shaped form when thetripod neighborhood is used (Fig. 10б). In all four cases there is a successful colonization of free habitat and the species exists indefinitely long.

Visualization 9. Model 3 with Moore neighborhood.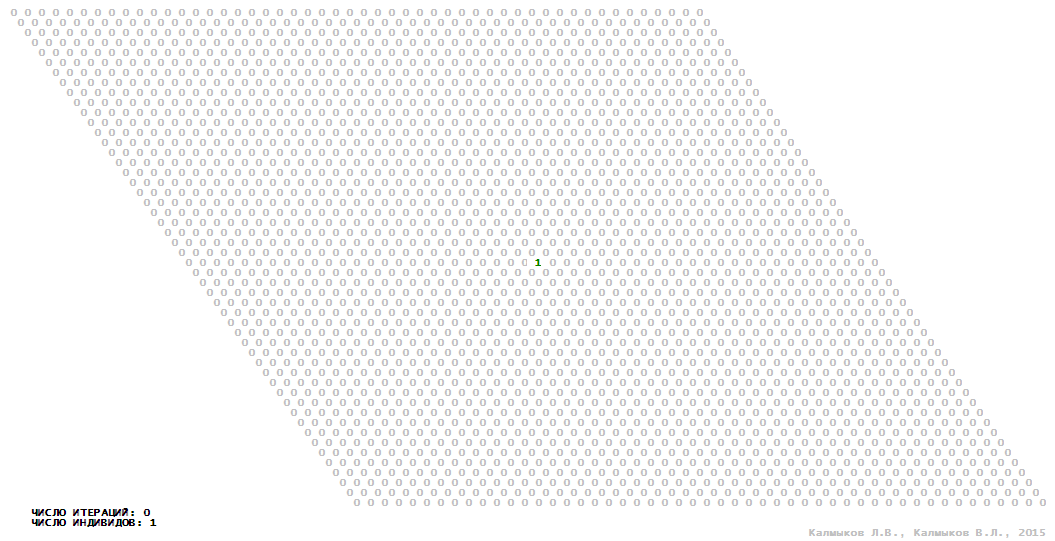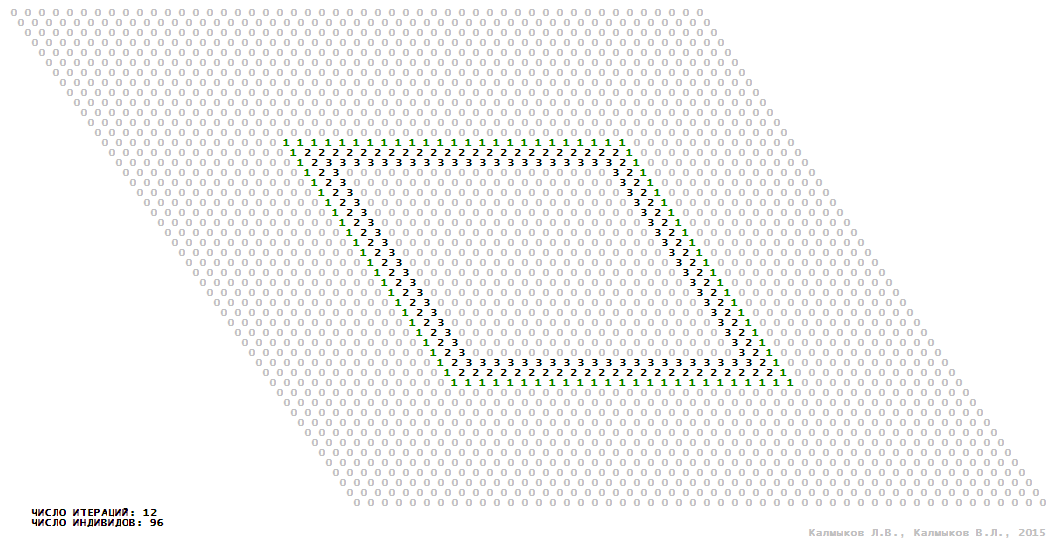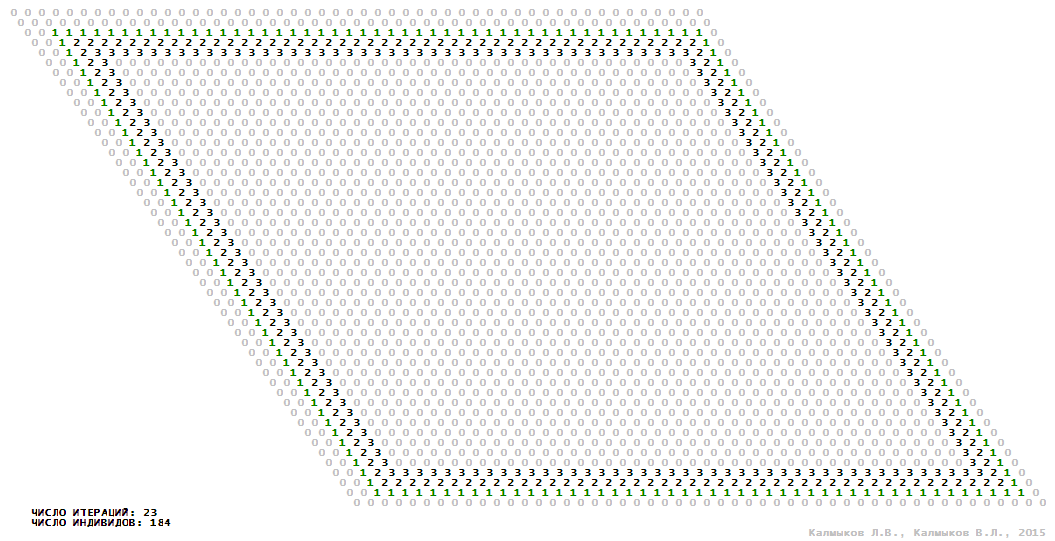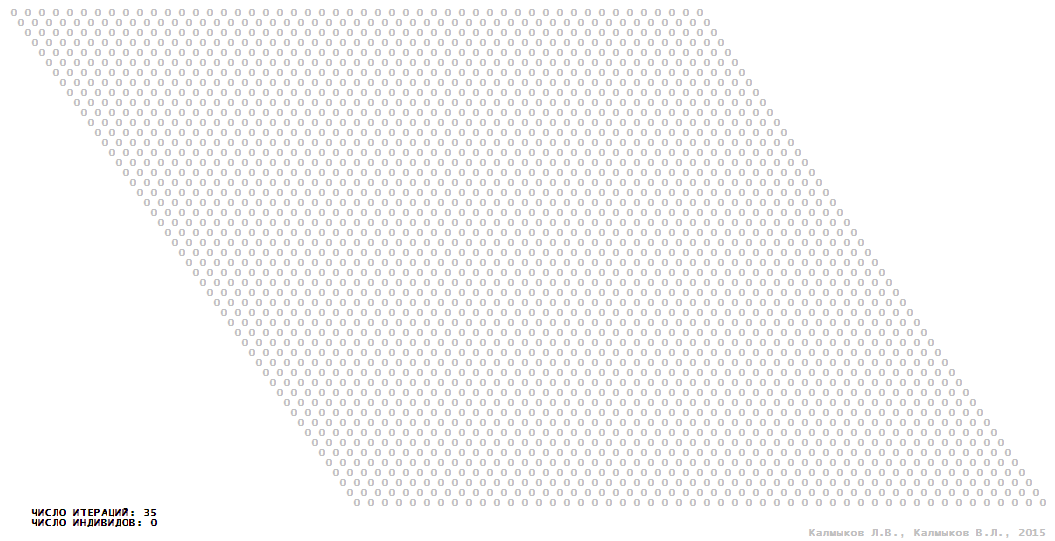

Visualization 10. Model 3 with hexagonal neighborhood.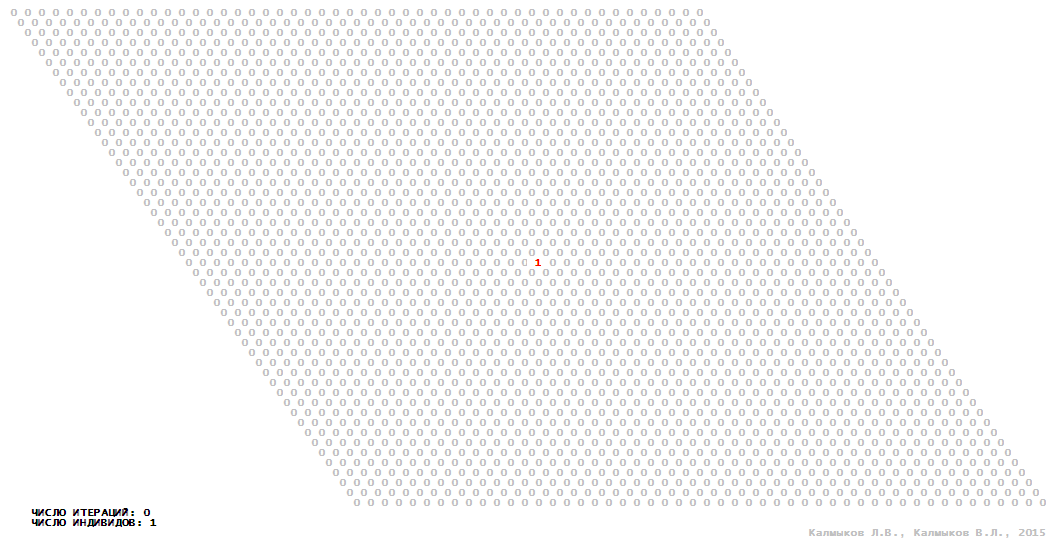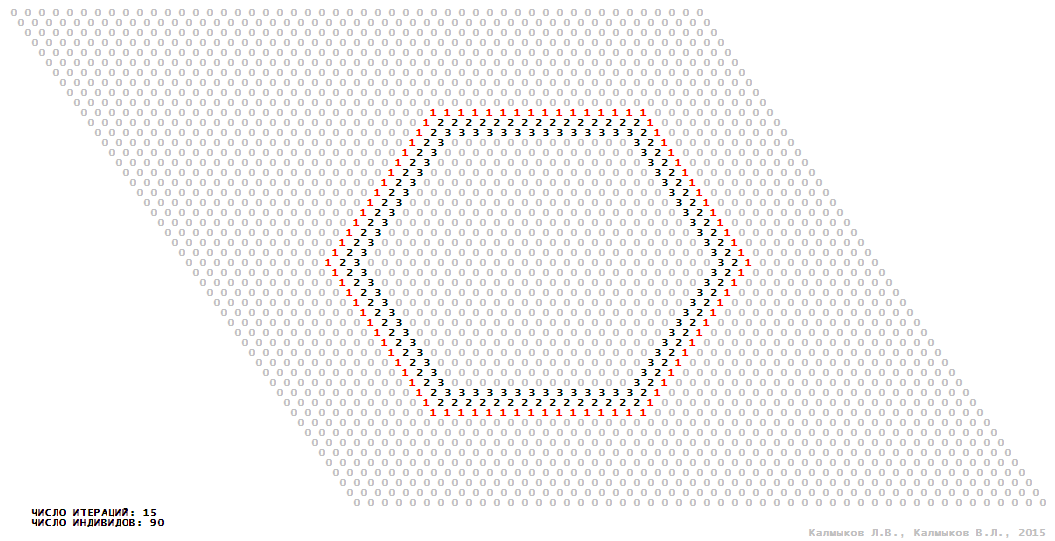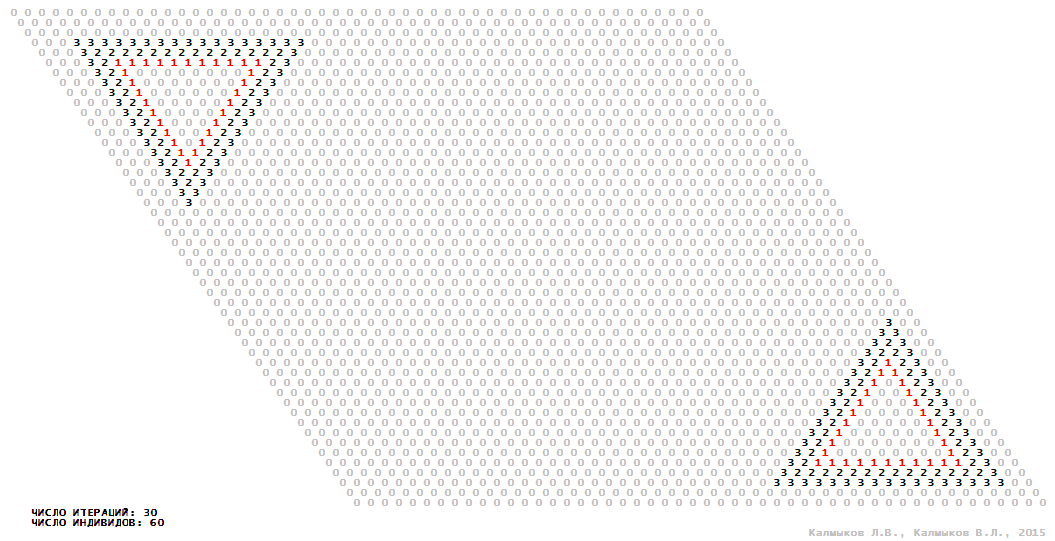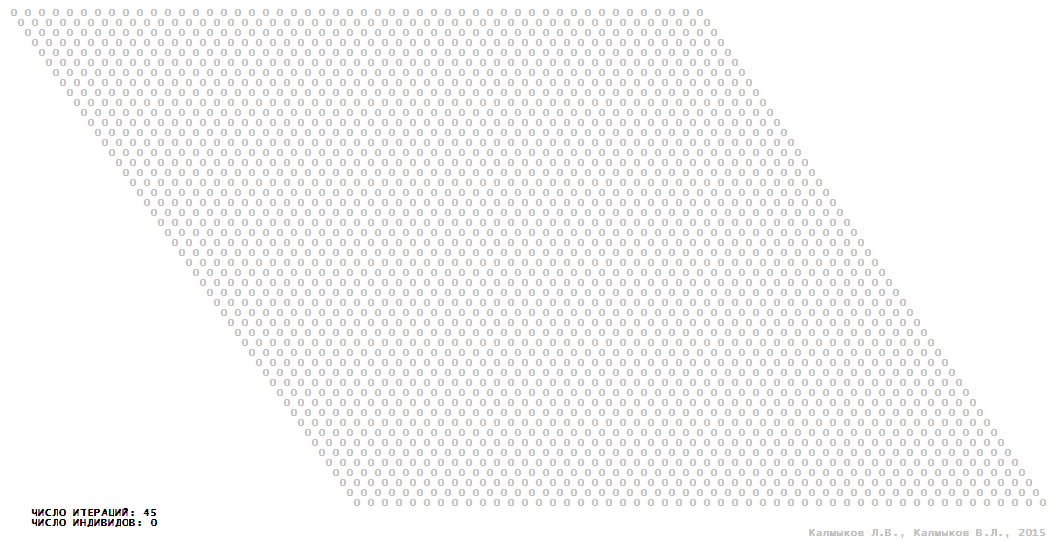

Visualization 11. Model 3 with von Neumann neighborhood.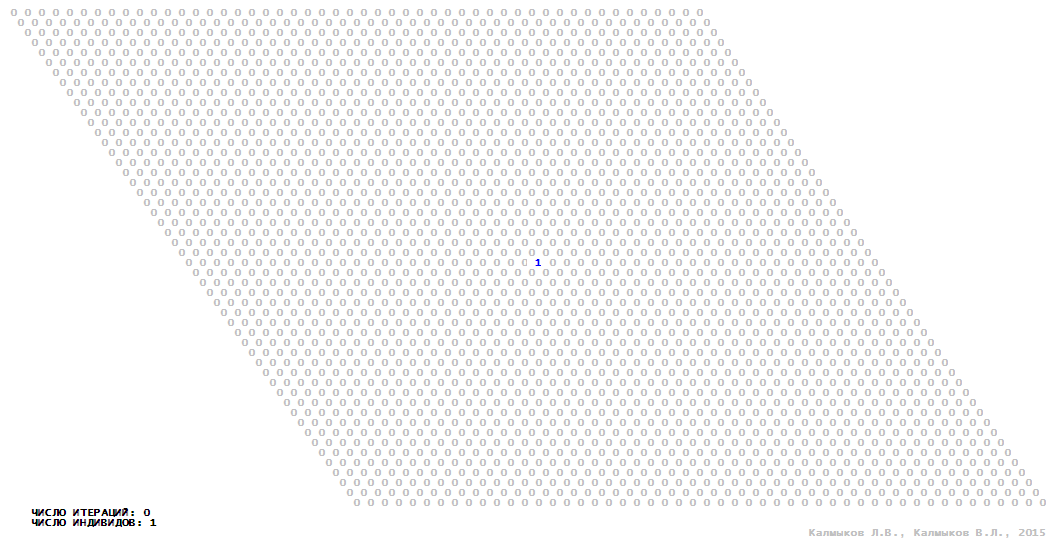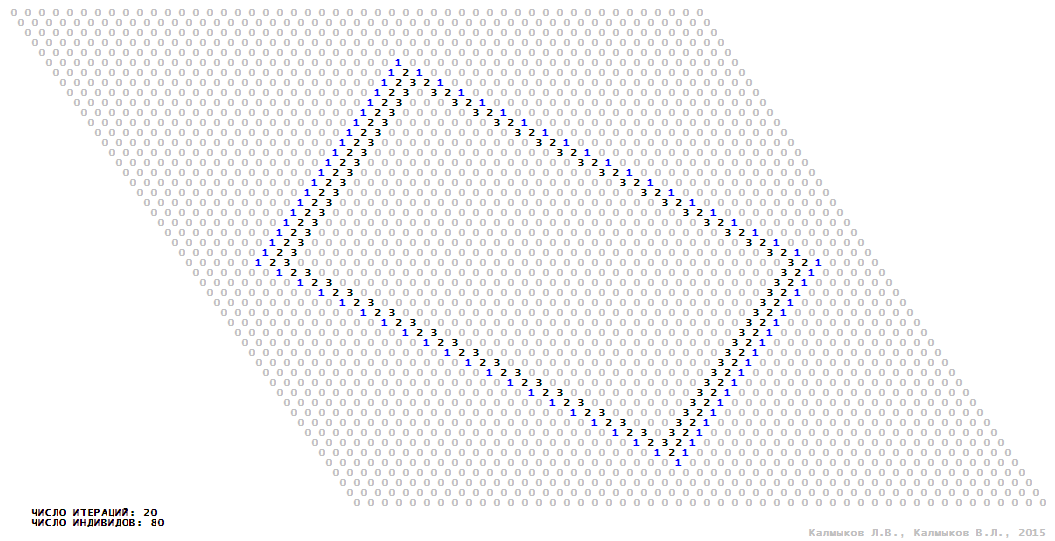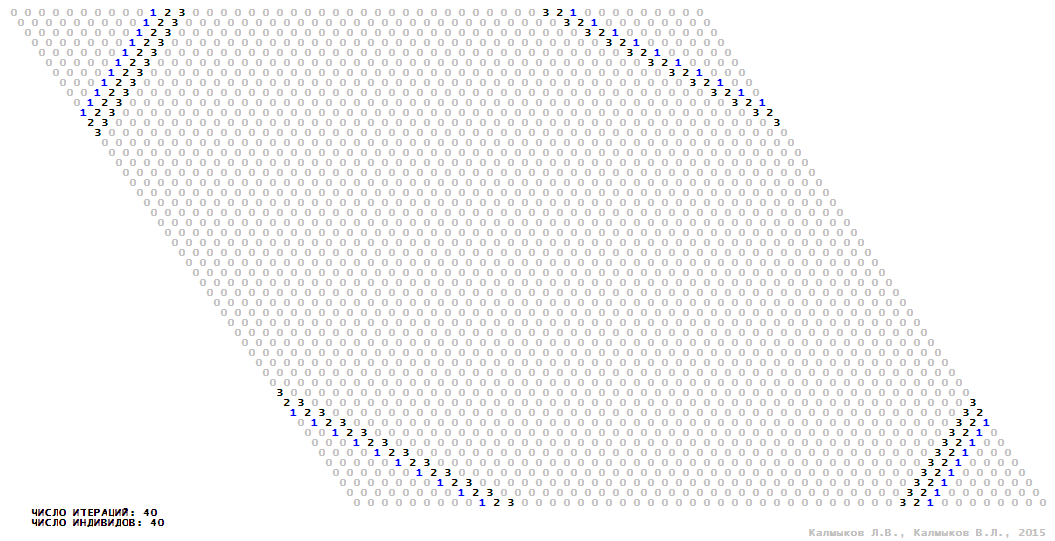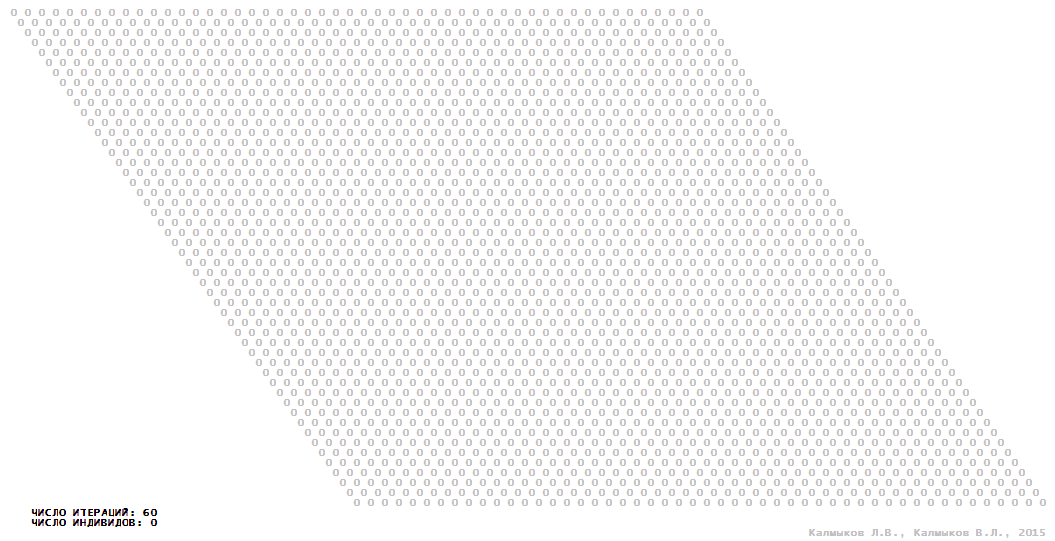

Visualization 12. Model 3 with tripod neighborhood.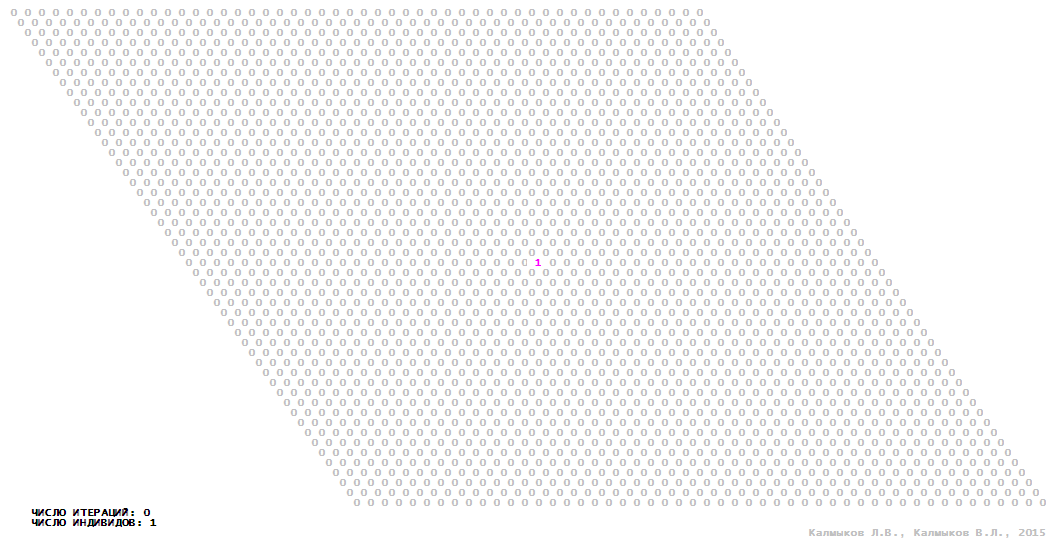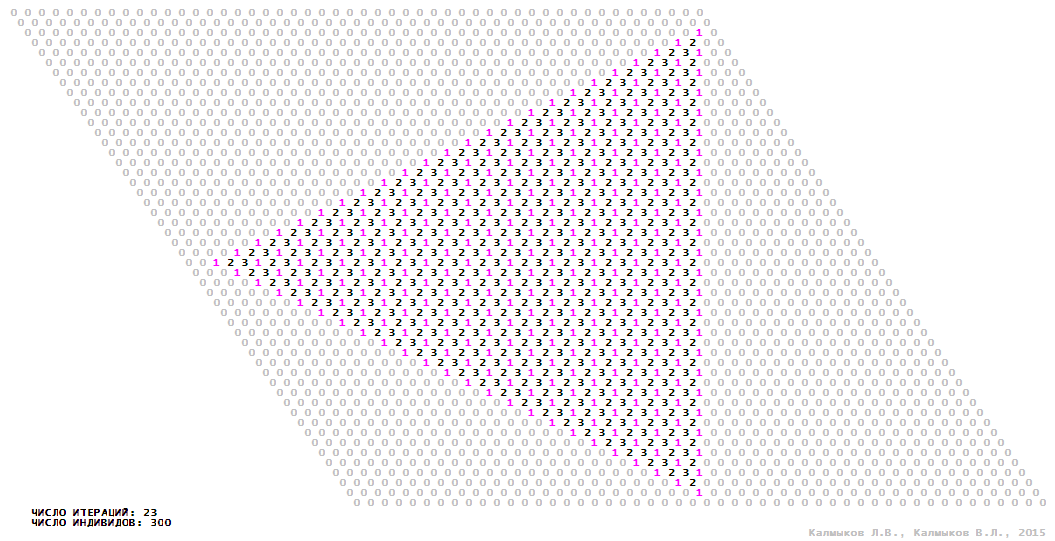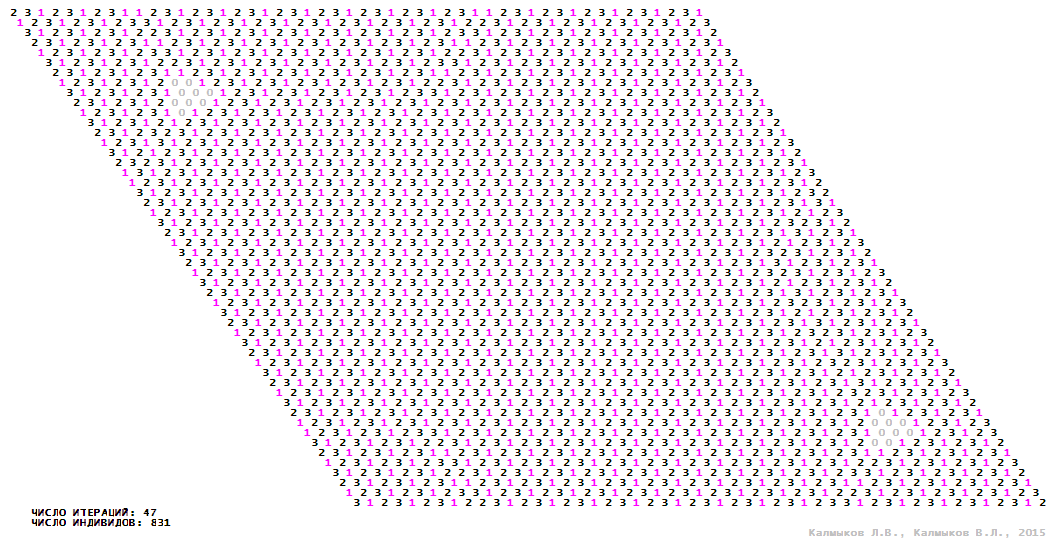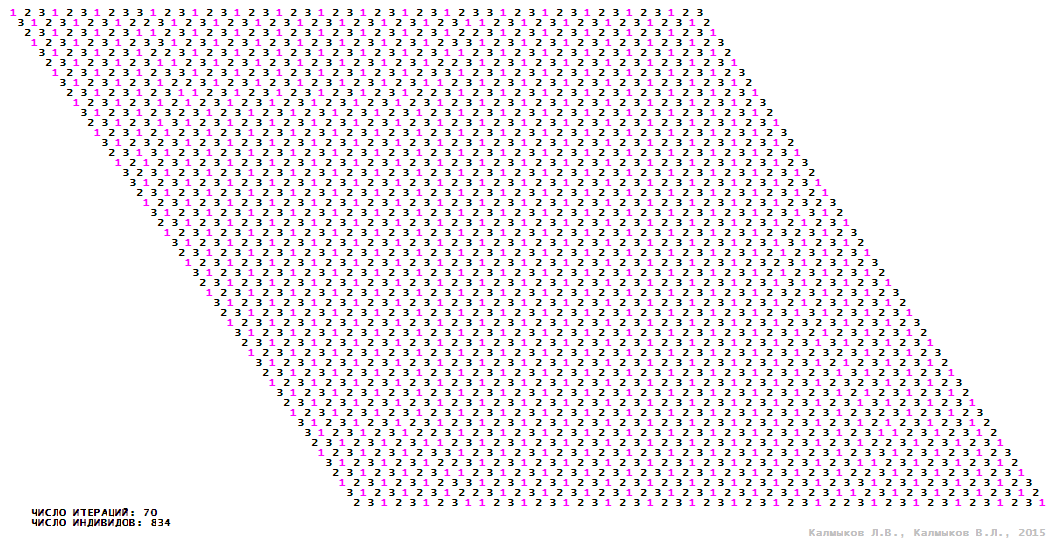

Model 3 (Visualizations 9–12) is a logical deterministic cellular automaton with four states. A set of possible states of each lattice site is {0, 1, 2, 3}. Cellular automaton lattice consists of 50x50 sites and it is closed by periodic conditions on the torus. Resource regeneration of a microhabitat including recycling of a dead individual takes two iterations. The following symbols are used to indicate the states of cellular automaton cell: {0} – a microhabitat is free; {1} – a microhabitat is occupied by an individual; {2, 3} – a microhabitat is in the regeneration state which takestwo iterations. Using various neighborhoods we investigate the impact of the number of offsprings and their positioning in space on population dynamics. Population growth curves show a linear growth, which is sharply replaced by decreasing of population number, leading to population extinction (Fig. 10в), i.e. a population catastrophe occur. The population catastrophe is occurred when Moore, hexagonal and von Neuman neighborhoods are used. Population growth curve has double S-shaped form whenthe tripod neighborhood is used (Fig. 10в). In this case a successful colonization of free habitat occured and species population continued to exist indefinitelylong.

Visualization 13. Model 4 with Moore neighborhood.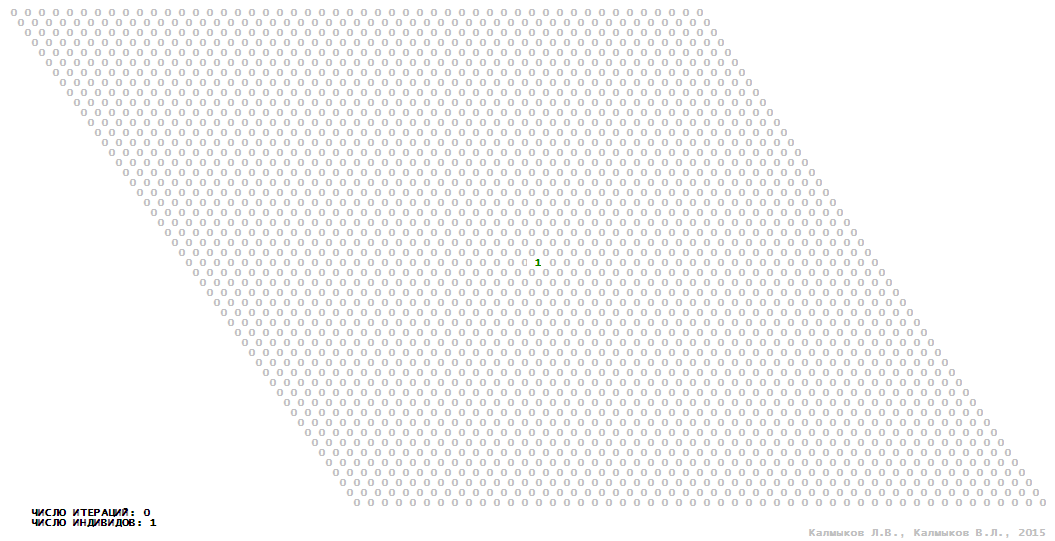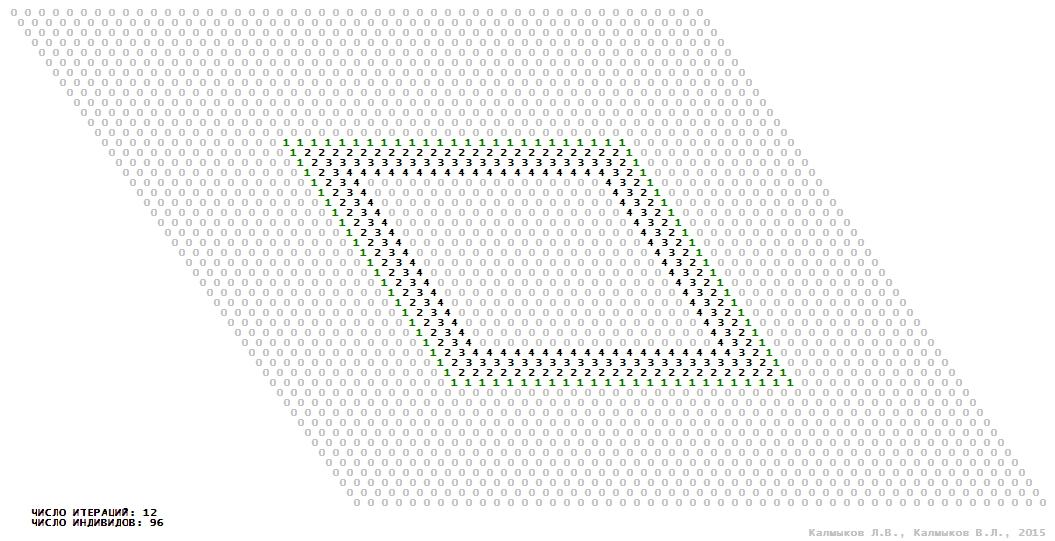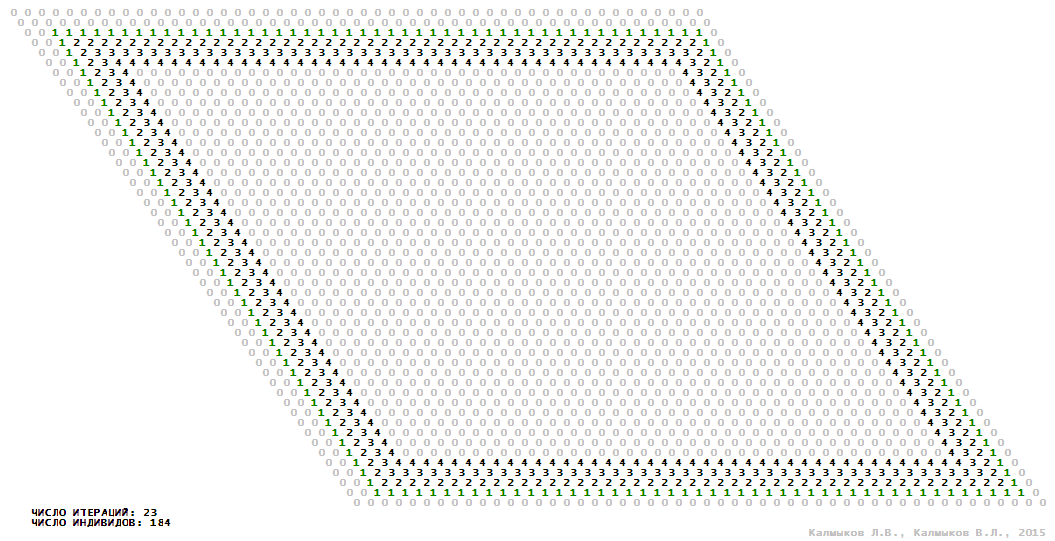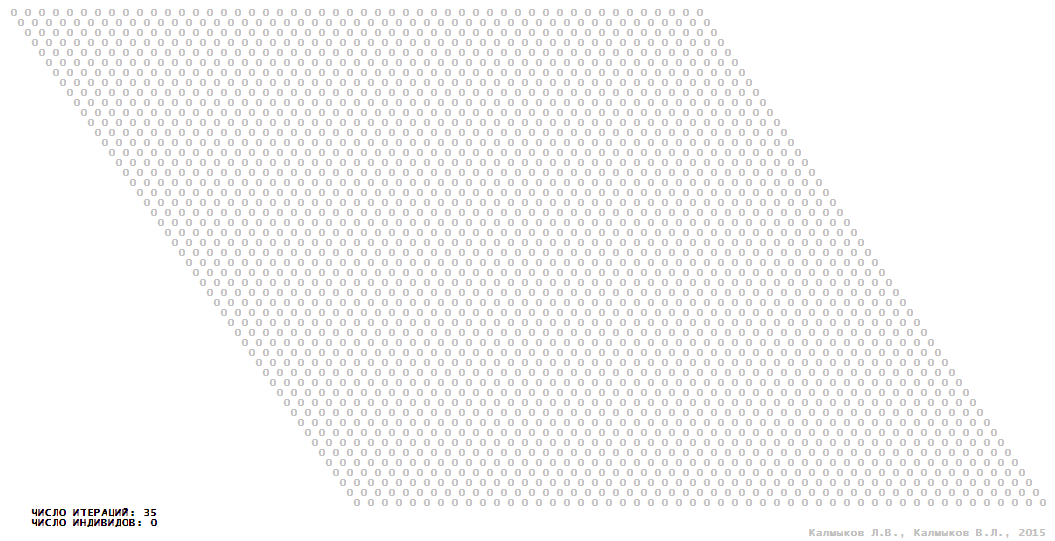

Visualization 14. Model 4 with hexagonal neighborhood.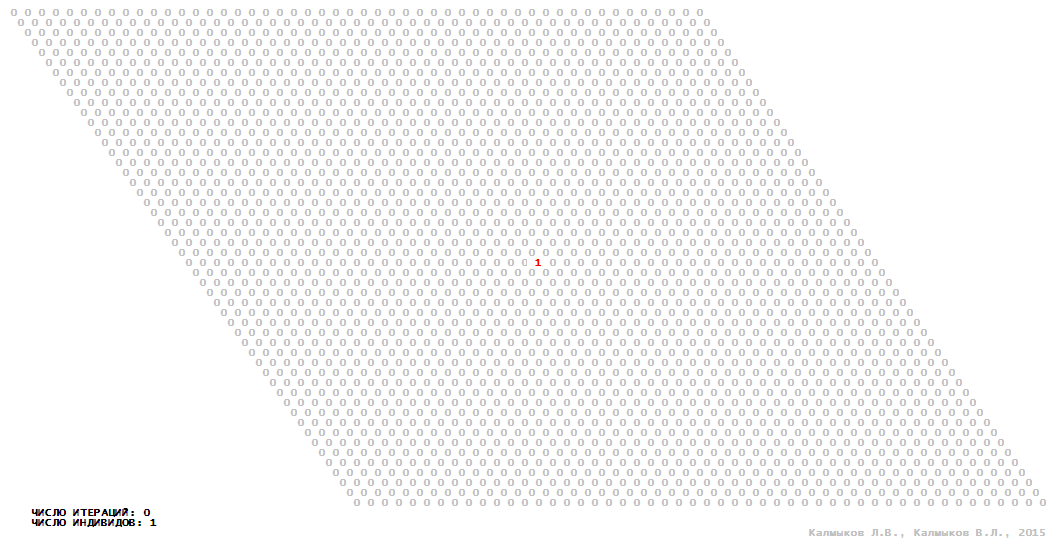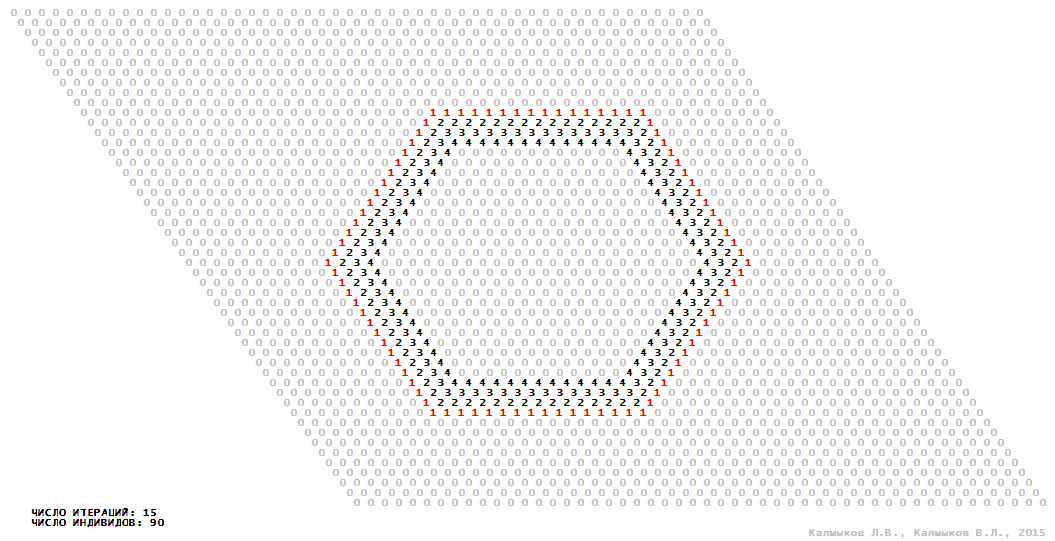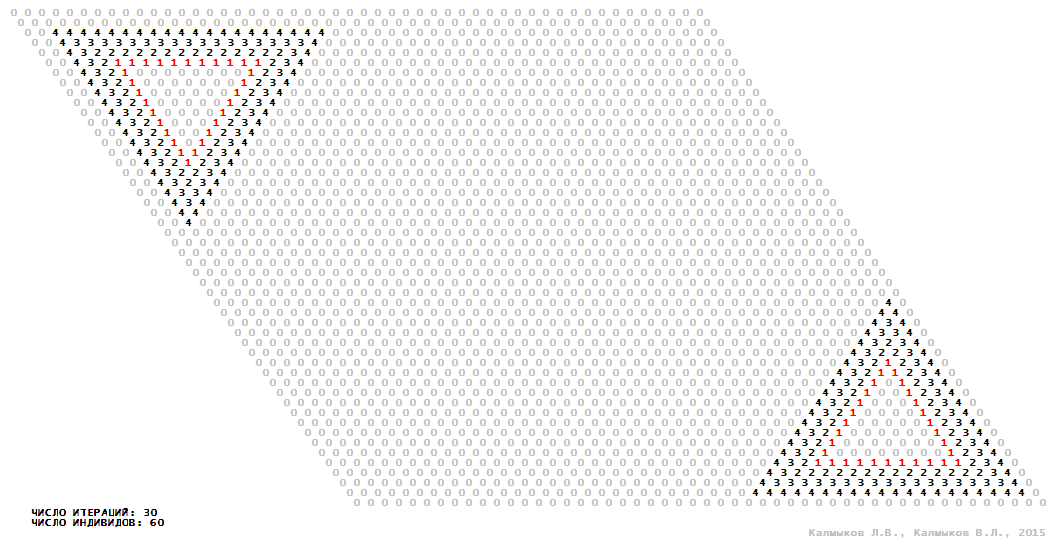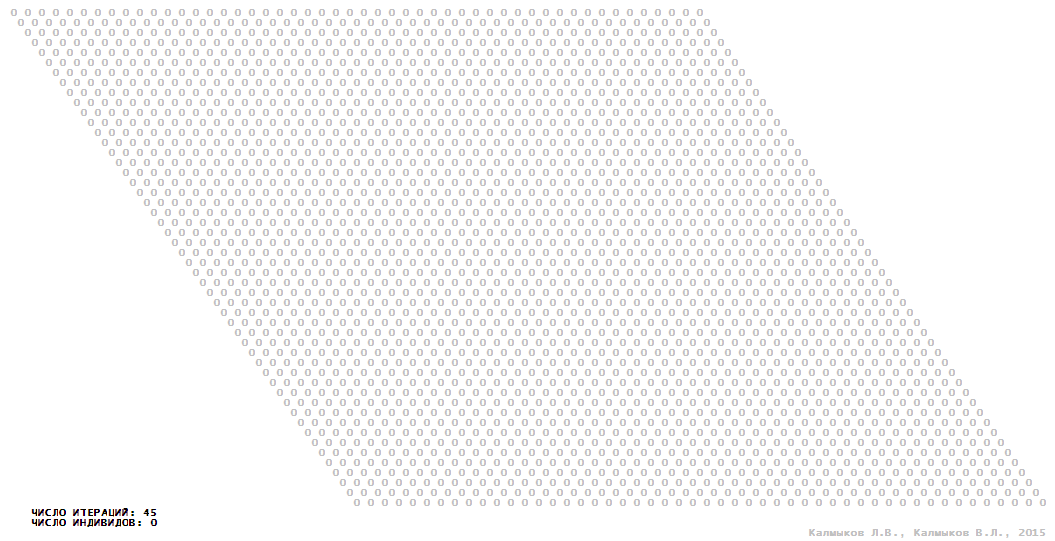

Visualization 15. Model 4 with von Neumann neighborhood.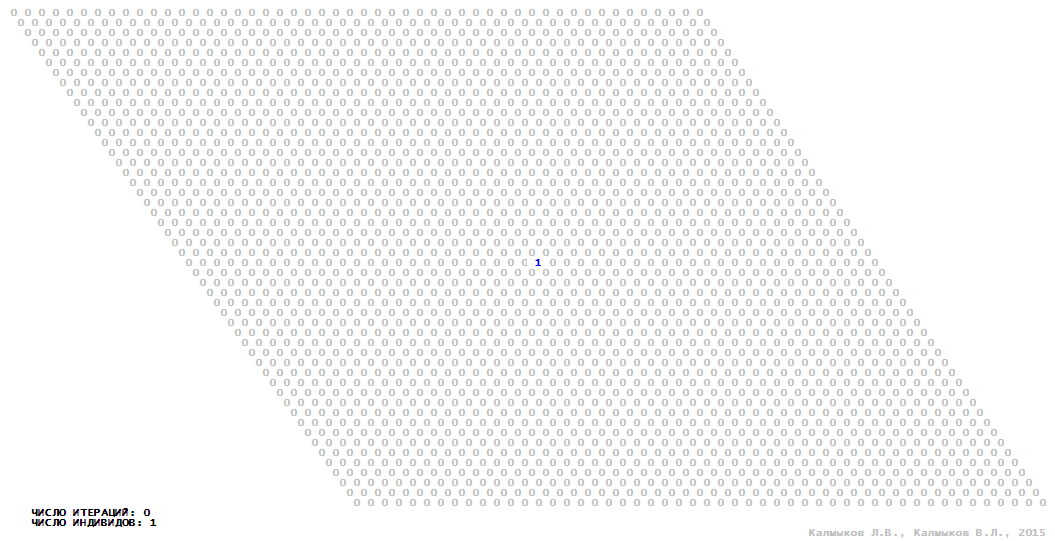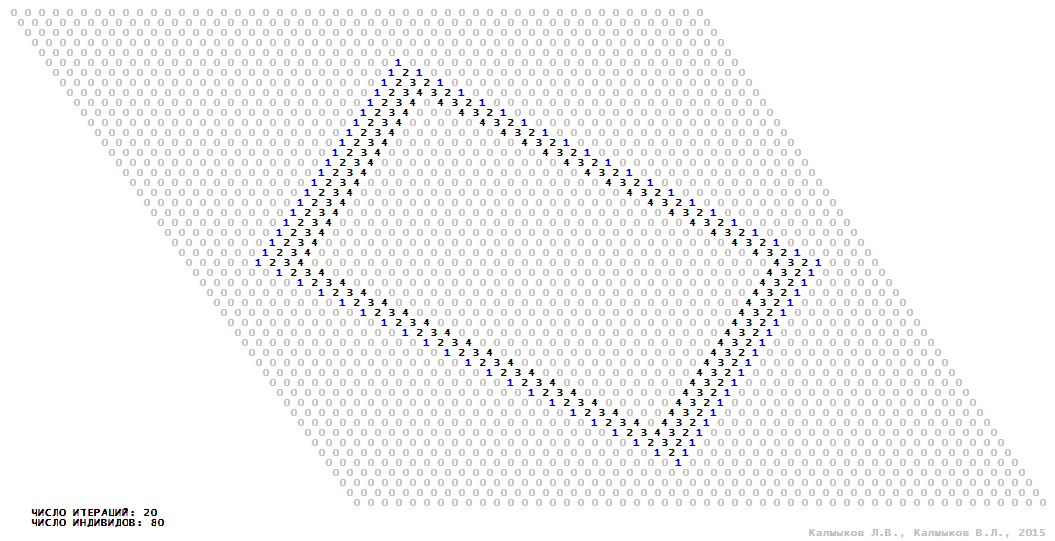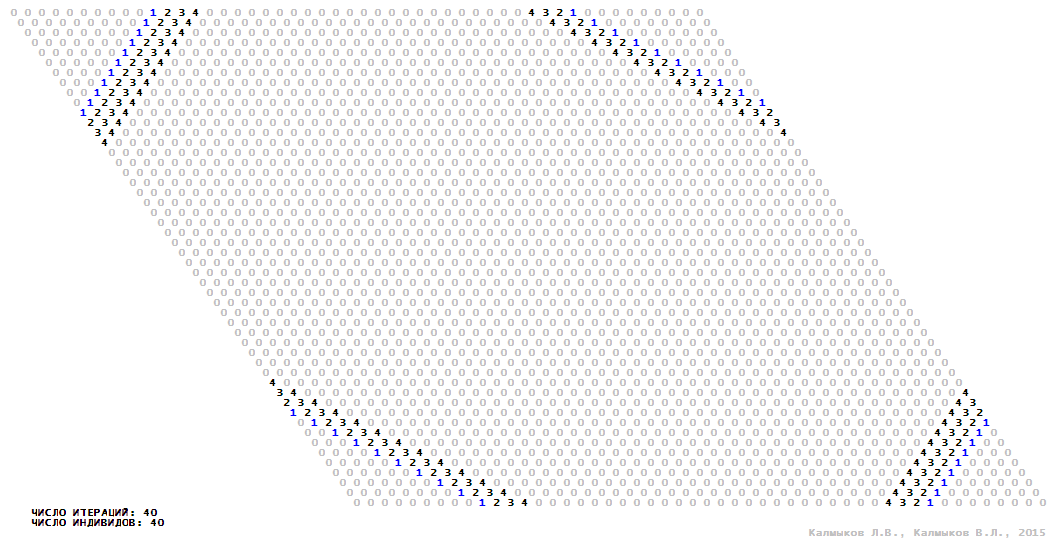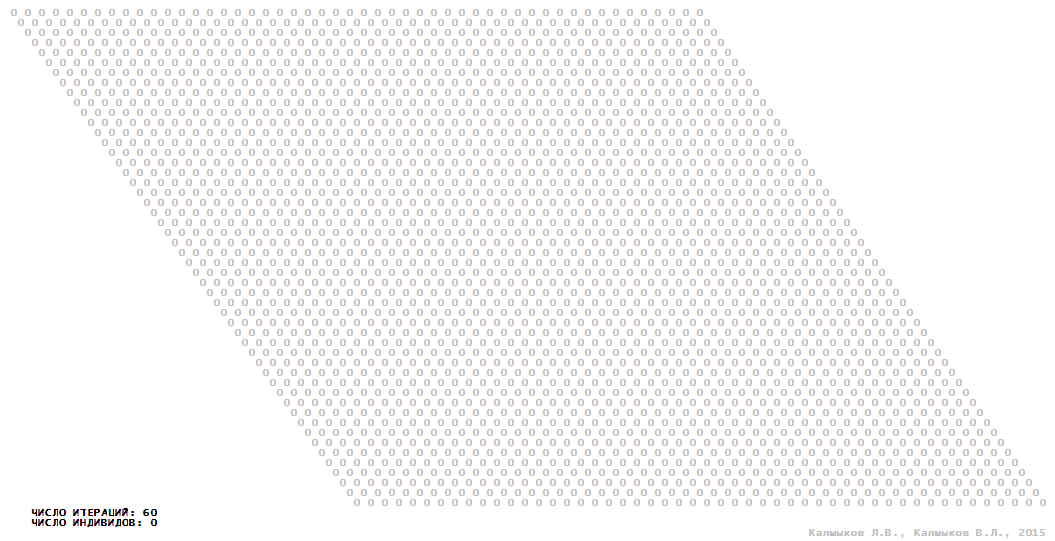

Visualization 16. Model 4 with tripod neighborhood.

Model 4 (Visualizations 13–16) is a logical deterministic cellular automaton with five states. A set of possible states of each lattice site is {0, 1, 2, 3, 4}. Cellular automaton lattice consists of 50x50 sites and it is closed by periodic conditions on the torus. Resource regeneration of a microhabitat including recycling of a dead individual takesthree iterations. The following symbols are used to indicate the states of cellular automaton cell: {0} – a microhabitat is free; {1} – a microhabitat is occupied by an individual; {2, 3, 4} – a microhabitat is in the regeneration state which takesthree iterations. Using various neighborhoods we investigate the impact of the number of offsprings and their positioning in space on population dynamics. In all four cases population growth curves show a linear growth, which is sharply replaced by decreasing of population number, leading to extinction of the populations, i.e. a population catastrophe occur (Fig. 10г).